Teorema di Rolle: enunciato, significato, esercizi e applicazione

Nella seconda prova della Maturità 2023 gli studenti del liceo scientifico sono stati chiamati a risolvere quesiti di matematica. Uno degli otto si risolveva con il Teorema di Rolle: ma di cosa si tratta?

Teorema di Rolle: enunciato

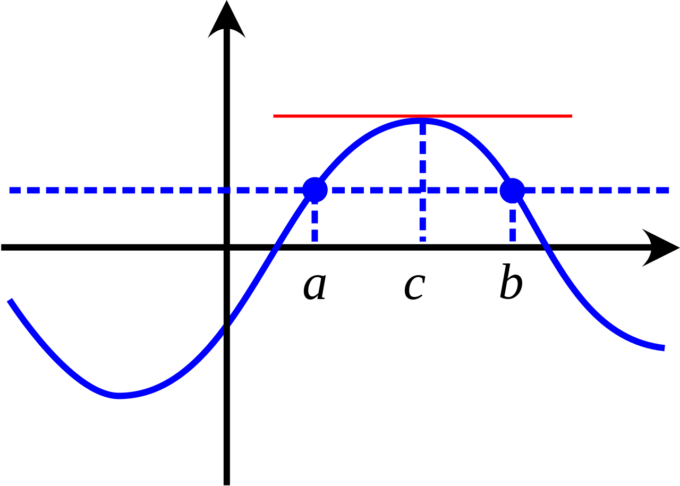
Il teorema di Rolle afferma che  "se una funzione è continua in un intervallo chiuso [a,b], è derivabile in ogni punto di tale intervallo, e assume valori uguali f(a)=f(b), esiste almeno un punto interno all'intervallo (a,b) la cui derivata si annulla (f'(c)=0)".

Di seguito un video con esercizi e applicazione:

Teorema di Rolle: la storia

Il teorema porta il nome del matematico francese Michel Rolle (nato ad Ambert il 21 aprile 1652  e morto a Parigi l'8 novembre 1719). Enunciò il suo teorema nel 1691  nel caso particolare dei polinomi reali ad una variabile.

Si deve inoltre a lui la corrente notazione standard per indicare la radice n-esima di X.

La conoscenza del teorema di Rolle è attribuita però al matematico indiano Bhaskara (1114–1185). La dimostrazione di Rolle, successiva di cinquecento anni, non usava i metodi del calcolo differenziale.

Il teorema fu per la prima volta provato da Cauchy nel 1823 come corollario della dimostrazione del teorema di Lagrange.  Il nome "teorema di Rolle" fu usato per la prima volta dal tedesco Moritz Wilhelm Drobisch nel 1834 e dall'italiano Giusto Bellavitis nel 1846.